【数学II】最大・最小問題

今回は最大・最小問題を扱います。

文字を置き換えることで，自分が既に知っている問題に帰着させることが大切です。また，文字を置き換えた直後に，新しく設定した文字の定義域を考える癖をつけるようにしましょう。

問題の式を見たときに，どこに着目して何を考えるのかが分かるようになることが重要です。

考え方

三角関数をみたときに最初に考えることは，主に次の2つです。

• $\sin$ や $\cos$ のどちらかで統一する。
• 角を揃える。

例えば，$\sin$ で統一できれば，$\sin\theta=t$ と置くことで $t$ の関数として考えることができます。ただし，$t$ はすべての実数値をとれないことに注意しましょう。

もし，$\theta$ がすべての実数値をとったとしても $-1\leqq\sin\theta\leqq1$ となります。
$\theta$ が取り得る値に範囲に応じて，$t$ が取り得る値が決定するため，それを調べることを忘れないようにしましょう。

今回の問題では，$\cos2\theta$ と $\cos\theta$ で $\cos$ で統一されていますが，角が $2\theta$ と $\theta$ で異なります。このままだと文字の置き換えができないため，角をどちらかに揃えることを考えます。一般的には，係数が小さい方に揃えることを考えます。

したがって，今回の場合，$\theta$ に揃えることを考えます。ということは，$\cos2\theta$ を $\cos\theta$ で表す方法を考えることになります。

2倍角の公式を利用することで，$\cos2\theta=2\cos^2\theta-1$ と $\cos\theta$ で表せますね。

このあとは，$\cos\theta=t$ とおくことで，与えられた関数は $t$ の2次関数となるため，定義域がある2次関数の最大最小問題を考えれば良いということです。

解答

$\cos2\theta=2\cos^2\theta-1$ より，

$\cos\theta=t$ とおくと，$0\leqq\theta<2\pi$ より，$-1\leqq\sin\theta\leqq1$

与えられた関数は

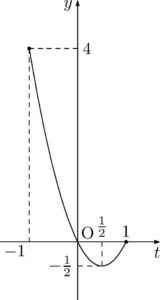
グラフより，$y$ は $t=-1$ のとき最大となり，$t=\dfrac{1}{2}$ のとき最小となる。

$t=-1$ のとき，$\cos\theta=-1$
$0\leqq\theta<2\pi$ より，$\theta=\pi$

$t=\dfrac{1}{2}$ のとき，$\cos\theta=\dfrac{1}{2}$
$0\leqq\theta<2\pi$ より，$\theta=\dfrac{\pi}{3},\dfrac{5}{3}\pi$

よって，求める最大値と最小値は次のようになる。

まとめ

今回の問題では，問題を見て最初に考えることとして，$\sin$ や $\cos$ に統一することや角を揃えることがパッと思い浮かべることができる状態になるまで問題を解いて慣れましょう。

良質な問題を解こうと思うがあまり，質を求める人がいますが，とりあえずは量を優先しましょう。多くの問題をこなすことで質が良くなっていきます。