LINE@などで質問された問題をシェアしていきます。
数学Iの不等式の文章題です。
数学Iの不等式の文章題です。
問題ある高等学校の1年生全員が長いすに座っていくとき,1脚に6人ずつかけていくと15人が座れなくなる。
また,1脚に7人ずつかけていくと,使わない長いすが3脚できる。長いすの数は何脚以上何脚以下か。
また,1脚に7人ずつかけていくと,使わない長いすが3脚できる。長いすの数は何脚以上何脚以下か。
考え方
基本的に1つのものと複数のものを対応させるときは,1つのものの数を $x$ と設定するとうまくいく可能性が高いです。
今回の場合は,1つの長いすに複数の生徒を座らせますから,長いすの数を $x$ としましょう。
問題文の「1脚に6人ずつかけていくと15人が座れなくなる」の部分から生徒数を $x$ で表すことができて,$(生徒数)=6x+15$ となります。
聞かれているのは長いすの数の取りうる値の範囲だから,不等式を立てることを考えます。
「1脚に7人ずつかけていくと,使わない長いすが3脚できる」の部分から生徒数の取りうる範囲を考えましょう。
解答
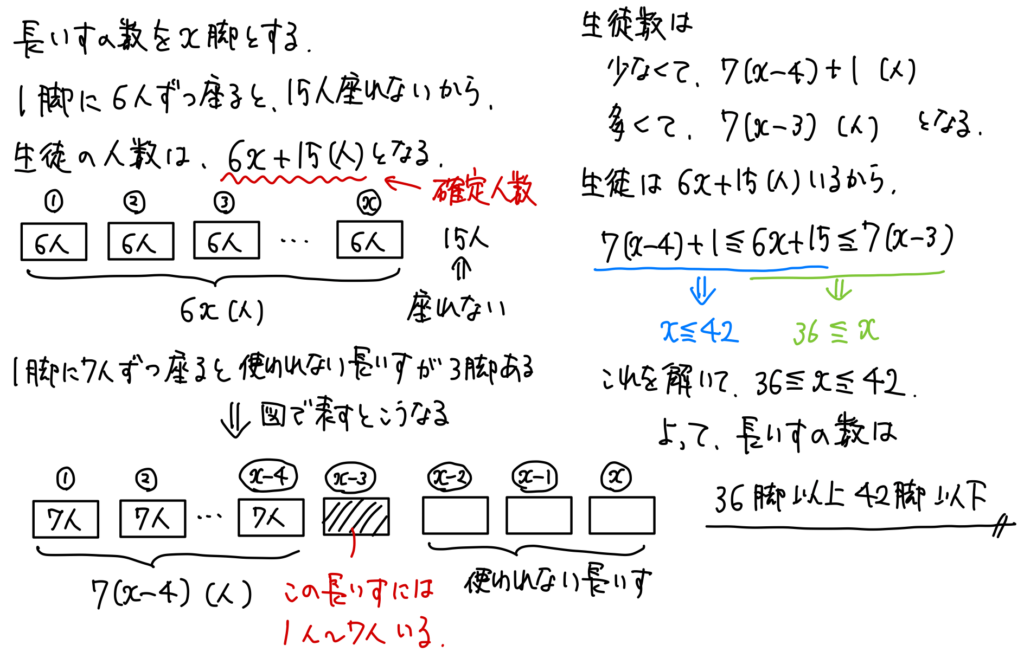
長いすの数を $x$ とすると,生徒数は $6x+15$ となる。
1脚に7人ずつかけていくと,使わない長いすが3脚できるから,
\begin{align*}
7(x-4)+1\leqq 6x+15\leqq7(x-3)
\end{align*}
これより7(x-4)+1\leqq 6x+15\leqq7(x-3)
\end{align*}
\begin{align*}
&7x-27\leqq6x+15\leqq7x-21 \\
&36\leqq x\leq42
\end{align*}
よって,長いすの数は36脚以上42脚以下。
&7x-27\leqq6x+15\leqq7x-21 \\
&36\leqq x\leq42
\end{align*}
より丁寧な手書き解答